⚙️ Engineering Principles: The Importance of Knowing the Basics

Engineering principles: Anatolii, a brilliant engineer from Australia that participated in the CEPSA challenge, explains the importance and the value of knowing the basics of engineering in order to be a good engineer. He has also included an example to illustrate how vital these engineering principles are.

Written by Anatolii Artamonov

If you are interested in engineering challenges, learn more about them in our recent challenges section.

Engineering Principles: Why they are important

If you deposit $1 on a savings account with 100% interest rate that is continuously compounded, at the end of a year you’ll get $2.71828 – irrational number that is known in mathematics as “e” – the base rate of growth shared by all continually growing processes or, as mathematicians say, the base of the natural logarithm.

Any continually growing system can be described scaling the base rate “e” just like we can describe any number scaling 10 (we widely use the decimal numeral system as opposed to digital electronics that rely on the binary numeral system). Similarly, the natural logarithm of a number X is how many years $1 needs to be on our 100% interest rate account to accumulate $X.

I have always been fascinated with such simple “high-level” explanations/analogies that give a simplified understanding of basic engineering principles. With such insights, it is far easier to work out details and ultimately deeper understanding of a concept. I also thought that such an approach to understanding concepts is predominantly confined to the academic world, whereas, in the real world, especially the industrial world, it is more about practical applications rather than insights of theoretical principles.

When I joined the industry as a young mechanical engineer, I was trying to apply that academic approach to better understand engineering concepts and their applications to effectively solve real-world problems. To my surprise, there were engineers who didn’t fully understand engineering concepts and were solving technical issues somewhat ineffectively.

I would like to share some examples of my own experience to reflect on this premise.

First case: The Bucket Elevator

The first example is about my experience at Calciner Plant in Northern Ontario, Canada where a Bucket Elevator (BE) was the plant’s bottleneck at the time. The Bucket Elevator’s main function is to deliver a product in the form of powder from one level up to the level above by buckets that are attached to a belt, which rotates around the top and bottom shafts, discharging powder from the buckets into the chute at the top of the BE. It limited production rates to 4 t/h. 

Increasing feed rate would rapidly increase driver motor power consumption and its subsequent trip on high current draw. Simplified graphical representation of the BE is depicted below: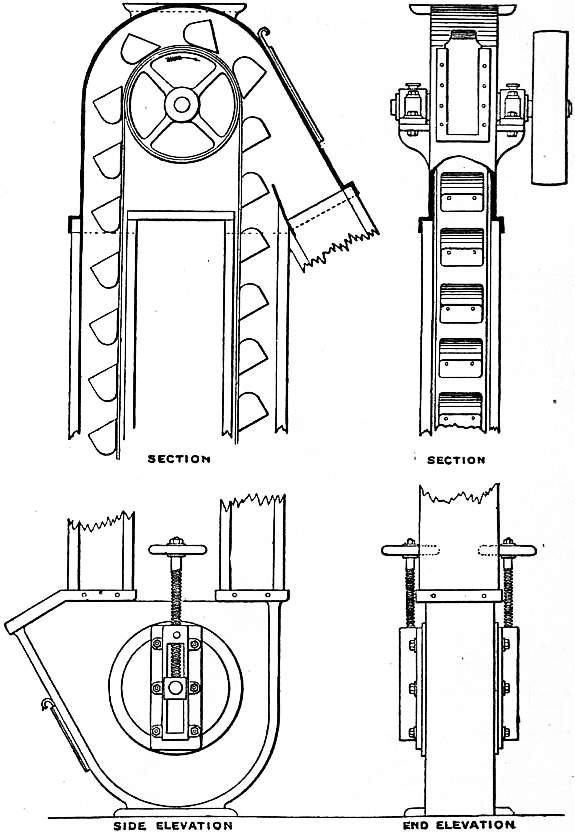 

Figure 1. Bucket Elevator. Source: https://en.wikisource.org/wiki/Page:EB1911_-_Volume_07.djvu/75

Several engineers tried to increase the Bucket Elevator operating capacity. They tried to modify the shape of the buckets, the shape of the discharge chute and the way the product is being loaded into the buckets. Some of them tried to increase the speed of the buckets, check all bearings and even consider upgrading the BE motor.

Although to some extent they all are relevant to the efficiency of the BE, none of them really solved the problem – the maximum continuous and sustainable feed rate still remained around 4 t/h.Luckily, I didn’t know anything about previous attempts to resolve the issue, otherwise, I would’ve been biased (I was told about them after the BE feed rate was successfully increased).

My first thought was: the product that is carried in the buckets is discharged at the top in the required direction by a combination of 2 forces - gravity and centrifugal force. If these forces are unbalanced, as one extreme, the product would be either dropping inside the BE not reaching discharge chute (speed of rotation is too slow) or, the other extreme, kept inside the buckets without being discharged into the chute (speed of rotation is too fast).

These were the basics. If the speed is right, then the problem is something else. For this reason, I filmed the discharged end of the BE through the inspection window and watched it in slow motion on a PC screen to see what actually happens when the buckets pass the discharge chute.

It was clear: the majority of the product is being carried in buckets and never dropped down causing all sorts of issues, including the motor trip. This simply meant that the speed was too fast. From now on, this became an easy task to solve: imagine a half-full cup of coffee which is quickly rotated by hand around a shoulder.

Would coffee be spilled? Well, it depends on how quickly the cup is rotated: too slow – and coffee will be spilled, too fast – and it’ll stay in the cup. Exactly the same scenario was happening in BE: the speed of rotation was too quick and the product was “trapped” inside the buckets.

Technically speaking – centrifugal force was too high, not allowing the product to free fall (pulled by gravity) in a critical moment when a bucket was approaching the discharge chute in order to escape bucket and continue having horizontal velocity falling into the discharge chute. I did some calculations and figured out that, at motor AC frequency between 35 Hz and 40 Hz, there should be an ideal speed to discharge full bucket of powder.

Luckily, BE motor had VFD (Variable Frequency Drive). Changing AC frequency, we empirically found that at 38 Hz literally all the material was being discharged from the buckets into the discharge chute. As a result, the processing rate was increased to continuous and sustainable 6 t/h (+50% to 4 t/h rate) with no significant effect on motor power. 7 t/h was trialed later on with a marginal increase in motor current draw.

Other process bottlenecks have appeared at this feed rate. 7 t/h was the limit set by the Government under the contract with the Company and Province’s Ministry of Environment. The ingenious example of the very same principle was used by James Dyson in 1978 when he invented the world’s first bagless vacuum cleaner: the use of centrifugal force to separate the dust out of the air. The very same principle is used to spin water from clothes at the end of the washing cycle in our washing machines.

And many other great inventions are based on the same principle. Everyone can demonstrate the principle just with a cup of coffee (make sure coffee is not too hot, otherwise if the rotation speed is too low, you’ll get some burns!)

Check out the ennomotive blog for more posts about engineering innovations, don’t miss out!

Second case:  A Counterintuitive Approach

Due to lack of 1-3/8’’ stud bolts that are to be used on ASME B16.5 DN350 CL600 flanges, some of them were to be replaced with 1-1/4’’ studs as a temporary replacement until correct fasteners arrived. This is a typical situation experienced in an industrial plant located in the middle of a desert in Western Australia.

 

Figure 2. Flanged joint with 1-3/8'' studs (Note: photo was taken when the correct studs had been installed)

The maintenance team that was replacing studs asked for a target torque 1-1/4’’ studs should’ve been tightened to. The maintenance engineer reply was: 1.1 times of 1-3/8’’ studs torque. The reasoning behind it was simple: in order to provide the equivalent compression, smaller studs would have to be tightened 138114 =1.1 times higher than bigger studs.

As intuitive as it sounds, this is not quite correct. Simply put, bolt torque is directly proportional to bolt diameter, the coefficient of friction and required bolt compression force (T=KDF - as per ASME PCC-1 - 2013 Appendix K), which can be easily derived from the basic physics formulas for frictional force Ff=µFN and force couple - torque relationship T=FD.

Provided both types of studs are of the same material and surface treatment, the smaller the diameter of a stud, the less torque required to tension the bolt in order to reach the required compression force. Of course, smaller diameter bolt tensile stress would be higher than the bigger diameter bolt stress, but if it is within the allowable limits, this is acceptable For this particular example, 1-1/4’’ studs should have been tightened to 1.1 times less torque than 1-3/8’’ studs.

Surely many readers would recall similar examples in their own fields of expertise to reflect on the idea that simple “high-level” explanations/analogies that give insights into concepts that are important tools for young engineers to develop a deep understanding of the different engineering fields. In sum, these tools are as equally important in the industrial world as they are in the academic one.

Share with us other basic engineering principles that helped you in the professional world and explore what ennomotive has to offer.

Hungry for engineering challenges? The ennomotive community of engineers has already solved the following:

• Preventing sand accumulation on railways across the desert
• Redefining the installation of tramway rails
• Designing a New modular and transportable factory

Remember to join our community of engineers if you want to discover and/or participate in amazing engineering challenges and apply basic engineering principles!