SHARE
⚙️ La importancia de los principios básicos de la ingeniería
Principios básicos de la ingeniería: Anatolii, un brillante ingeniero de Australia que participó en el reto CEPSA, explica la importancia y el valor de conocer los principios básicos de la ingeniería para ser un buen ingeniero. También ha incluido un ejemplo para ilustrar lo vitales que son estos principios de la ingeniería.
Escrito por Anatolii Artamonov
Si te interesan los retos de ingeniería, aprende más sobre ellos en nuestra sección de desafíos recientes.
Principios básicos de la ingeniería: ¿Por qué son importantes?
Si ingresas 1$ en una cuenta de ahorro con una tasa de interés del 100% capitalizada continuamente, al final del año tendrás $2.71828 – número irracional conocido en matemáticas como “e” – la tasa de crecimiento básica de todos los procesos de crecimiento continuo o, como dicen los matemáticos, la base del logaritmo natural.
Un sistema de crecimiento continuo se consigue al escalar la tasa básica "e" de la misma forma que conseguimos cualquier número al escalar 10 (generalmente utilizamos el sistema numérico decimal, al contrario que de la electrónica digital, que utiliza el sistema numérico binario). De la misma forma, el logaritmo natural de un número X equivale a los años que 1$ tiene que pasar en la cuenta con una tasa de interés del 100% para llegar a X$.
Siempre me han resultado fascinantes las explicaciones / analogías simples "de alto nivel" que permiten comprender principios básicos de ingeniería. Con estos conocimientos es mucho más sencillo centrarse en los detalles y, en última instancia, profundizar en la comprensión de un concepto. Yo pensaba que esta forma de entender conceptos pertenecía únicamente al mundo acádemico mientras que, en el mundo real, sobre todo en la industria, nos centramos únicamente en las aplicaciones prácticas de los principios teóricos.
Cuando comencé a trabajar en la industria, cuando era un joven ingeniero mecánico, intenté aplicar dicho enfoque académico para comprender mejor los conceptos de ingeniería y sus aplicaciones para resolver problemas del mundo real. Para mi sorpresa, conocí ingenieros que no entendían del todo conceptos de la ingeniería y que resolvían problemas técnicos de una manera un tanto ineficiente.
Me gustaría ahora compartir algunos ejemplos de mi experiencia personal para reflexionar en torno a esta premisa.
Primer caso: el elevador de cubos
El primer ejemplo tiene que ver con mi experiencia en la planta Calciner en el norte de Ontario, Canadá, donde el elevador de cubos se había convertido en un cuello de botella. La función principal del elevador de cubos es transportar un producto en forma de polvo desde un nivel hasta el nivel superior mediante cubos unidos a una cinta que gira en torno a los ejes superior e inferior. Finalmente, los cubos vierten el polvo en una canaleta en la parte superior del elevador. La tasa de producción estaba limitada a 4 t/h.
Un aumento de la tasa de alimentación suponía el aumento rápido del consumo eléctrico del motor y, en consecuencia, la alta corriente desactivaba el motor. La siguiente imagen muestra una reprentación del elevador de cubos:
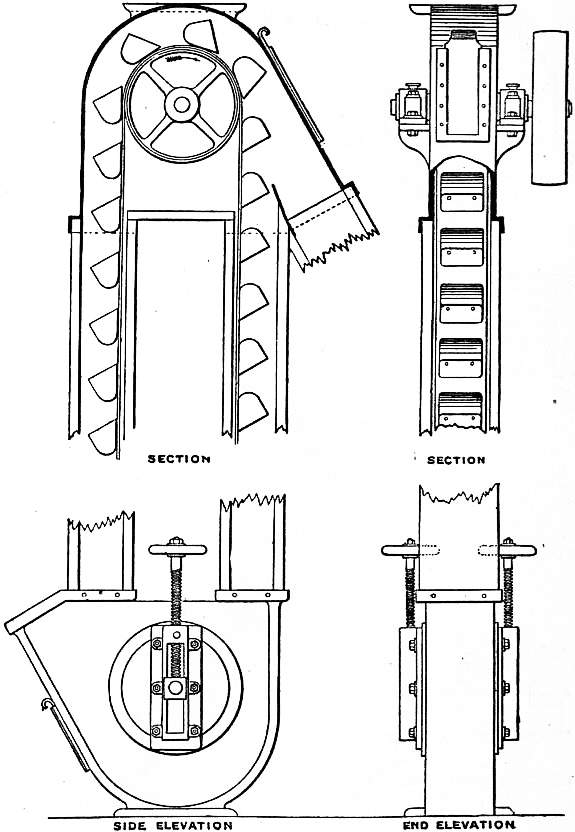
Imagen 1. Elevador de cubos. Fuente: https://en.wikisource.org/wiki/Page:EB1911_-_Volume_07.djvu/75
Varios ingenieros intentaron incrementar la capacidad operativa del elevador de cubos. Trataron de modificar la forma de los cubos, la forma de la canaleta y la forma en que llenaban los cubos. Algunos intentaron acelerar la velocidad de los cubos, comprobar los rodamientos e incluso se plantearon mejorar el motor del elevador de cubos.
Aunque todas estas opciones son relevantes hasta cierto punto para mejorar la eficiencia del elevador, ninguna solucionaba el problema real - la tasa de alimentación máxima continua y sostenible seguía en torno a las 4 t / h. Por suerte, yo no sabía nada de los intentos previos de resolver el problema, ya que me habrían condicionado (me hablaron de ello una vez se incrementó con éxito la tasa de alimentación del elevador de cubos).
Mi primer pensamiento fue: el producto de los cubos se vierte en la parte superior en la dirección adecuada gracia a la combinación de dos fuerzas, la gravedad y la centrífuga. Si una de estas fuerzas se desequilibra, o bien el producto queda vertido en el elevador y no en la canaleta - la velocidad de rotación es demasiado lenta - o, de lo contrario, el producto permanece en los cubos sin ser vertido en la canaleta - la velocidad de rotación es demasiado rápida.
Estos eran los conceptos básicos. Si la velocidad es la correcta, el problema surge de otra parte. Por esta razón, grabé la canaleta del elevador desde la ventana de inspección y pude observar a cámara lenta en la pantalla de un ordenador qué ocurría en realidad cuando los cubos pasaban junto a la canaleta.
Ya no había duda: la mayor parte del producto de los cubos no se vertía, lo que causaba todo tipo de problemas, incluyendo la desactivación del motor. Por lo tanto, la velocidad era demasiado rápida. A partir de ese momento, el problema tenía una fácil solución: imagina hacer círculos con el brazo con una taza de café medio llena en la mano.
¿Se derramaría el café? Bueno, depende de la velocidad en que la taza da vueltas: demasiado lento y el café se derrama, demasiado rápido y el café permanece en la taza. Le ocurría exactamente lo mismo al elevador: la velocidad de rotación era demasiado rápida y el producto quedaba "atrapado" en los cubos.
Técnicamente, la fuerza centrífuga era demasiado alta y no le permitía al producto caer, atraído por la gravedad, en el momento crítico en que el cubo se aproximaba a la canaleta y continuaba con la velocidad horizontal mientras el polvo caía en la canaleta. Realicé unos cálculos y descubrí que, con un motor de corriente alterna con una frecuencia entre 35 Hz y 40 Hz, la velocidad debería ser ideal para verter el cubo de polvo entero.
Por suerte, el elevador de cubos tenía frecuencia de accionamiento variable. Al cambiar la frecuencia de la corriente alterna, descubrimos empíricamente que a 38 Hz todo el material se vertía desde el cubo a la canaleta. Como resultado, la tasa de procesamiento se incrementó de manera continua y sostenible a 6 t / h (un 50% más que la tasa de 4 t/h) sin cambios significativos en la potencia del motor. Más adelante se hizo un intento para llegar a las 7 t/h con un aumento marginal en el consumo de corriente del motor.
También aparecieron otros cuellos de botella en el proceso con esta tasa de alimentación. Además, el límite impuesto por el Gobierno por contrato con la empresa y el Ministerio de Medio Ambiente de la provincia era de 7 t / h. Otro ejemplo ingenioso del mismo principio lo puso James Dyson en 1978 cuando inventó las primeras aspiradoras sin bolsa: utilizó la fuerza centrífuga para separar el polvo del aire. También es el mismo principio que se utiliza en las lavadoras para eliminar el agua al final del ciclo de lavado.
Cualquiera puede hacer una demostración de este principio con una taza de café, solo asegúrate de que el café no está demasiado caliente porque, si la velocidad de rotación es demasiado baja, ¡te quemarás!
Segundo caso: Un enfoque contradictorio
Debido a la falta de pernos roscados 1-3/8’’ que se usan en las bridas ASME B16.5 DN350 CL600, se tuvieron que sustituir temporalmente algunos de ellos por pernos 1-1/4’’ hasta que llegara la sujeción correcta. Esta situación es típica en una planta industrial situada en mitad del desierto en Australia occidental.

Imagen 2. Unión embridada con pernos 1-3/8'' studs (Nota: la foto fue tomada con los pernos correctos instalados)
El equipo de mantenimiento que estaba reemplazando los pernos preguntó a qué par de torsión deberían apretarse los pernos de 1-1 / 4 '’. La respuesta del ingeniero de mantenimiento fue: 1.1 veces el par de torsión de los pernos de 1-3 / 8 ". El razonamiento era simple: para proporcionar una compresión equivalente, los pernos más pequeños tendrían que apretarse 138114 = 1.1 veces más que los pernos más grandes.
Aunque parezca lógico, esto no es del todo correcto. En pocas palabras, el torque del tornillo es directamente proporcional al diámetro del tornillo, el coeficiente de fricción y la fuerza de compresión requerida del tornillo (T = KDF, según ASME PCC-1 - 2013 Apéndice K), que puede derivarse fácilmente de las fórmulas físicas básicas para fuerzas de fricción: Ff = µFN y par de fuerza - relación de par: T = FD.
Dado que los dos tipos de pernos están hechos del mismo material y han recibido el mismo tratamiento en la superficie, cuanto más pequeño sea el diámetro del perno, menor es el "torque" necesario para tensar el perno y alcanzar la fuerza de compresión requerida. En este ejemplo, los pernos 1-1/4’’ deberían haberse apretado 1,1 veces menos "torque" que los pernos 1-3/8’’.
Estoy seguro de que muchos lectores recordarán ejemplos similares en sus respectivos campos. Estas explicaciones o analogías simples y "de alto nivel" son realmente herramientas muy importantes para que los ingenieros jóvenes comprendan en profundidad las distintas ramas de la ingeniería. En resumen, estas herramientas son tan importantes en el mundo industrial como en el académico.
Cuéntanos qué conceptos básicos de ingeniería te resultaron de ayuda en el ámbito profesional y descubre qué mas puede hacer ennomotive por ti.
¿Hambriento de retos de ingeniería? La comunidad de ingenieros de ennomotive ya ha resuelto los siguientes:
- Evitar la acumulación de arena en las vías férreas que atraviesan el desierto
- Redefinir la instalación de raíles de tranvía
- Diseñar una nueva fábrica modular y transportable
Únete a nuestra comunidad de ingenieros si quieres descubrir y/o participar en increíbles retos de ingeniería y aplicar principios básicos de ingeniería.
